1. В простейшем случае "мотор" электродинамического громкоговорителя состоит из магнитной системы (магнит+магнитопровод) и звуковой катушки (каркас+намотанный на него провод). При протекании тока через звуковую катушку на нее действует сила Ампера (F=B*L*I), приводящая ее в движение. Здесь B — индукция магнитного поля в зазоре, L— часть длины провода катушки, находящаяся в зазоре магнитопровода, I— ток через катушку. Вроде все просто и прозрачно. Если бы не одно но, появляющееся при более пристальном взгляде на физические свойства магнитопровода...
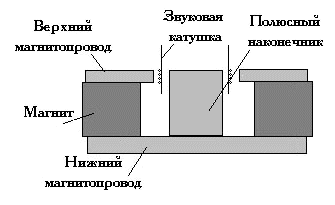
Рис.1.
С точки зрения схемотехника звуковая катушка (ЗК) фактически
представляет собой обычную индуктивность с ферромагнитным сердечником/магнитопроводом,
имеющим некоторое постоянное подмагничивание. Поэтому, как и положено индуктивности,
с ростом частоты импеданс ЗК возрастает, из-за возрастания вклада ее реактивного
сопротивления в общий импеданс ЗК. На низких частотах импеданс динамика также
возрастает из-за влияния основного механического резонанса его подвижной системы
через противо-ЭДС, наводящуюся в ЗК. Но в рамках данной статьи поведение импеданса
динамика на низких частотах нас не интересует. Гораздо интереснее заняться
рассмотрением влияния нелинейных магнитных свойств ферромагнитного сердечника
на индуктивность ЗК на средних и высоких частотах, там, где вклад индуктивности
в общий импеданс становится значительным. Еще более упростим себе задачу тем,
что не будем рассматривать нелинейность, возникающую из-за механического изменения
положения ЗК относительно магнитной системы динамика при его работе.
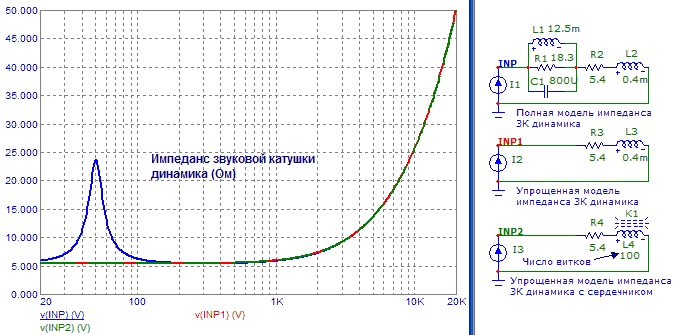
Рис.2. Электрическая модель динамика
2. Согласно формуле, сила Ампера F линейно зависит от тока
I, протекающего через ЗК. А так как ток через катушку при использовании источника
напряжения с низким выходным сопротивлением (например, УМЗЧ) по закону Ома
в основном зависит от импеданса этой катушки, то и возможная нелинейность
"мотора" будет также определяться амплитудной нелинейностью импеданса
звуковой катушки. Откуда же она может взяться, эта нелинейность?
Прояснить задачу нам поможет моделирование с помощью симулятора,
который позволяет вводить в схемы модели реальных магнитных цепей. Рассмотрим
поведение катушки с подобным сердечником в переменном магнитном поле. Пока
абстрактно. Как известно, индукция магнитного поля (МП) в сердечнике имеет
участки насыщения и характеризуется гистерезисом, при котором
кривые намагничивания и размагничивания не совпадают. На участках насыщения
сердечника индуктивность катушки падает, так как эффективная магнитная проницаемость
сердечника уменьшается. Это приводит к броскам переменного тока в цепи катушки
в моменты насыщения сердечника.
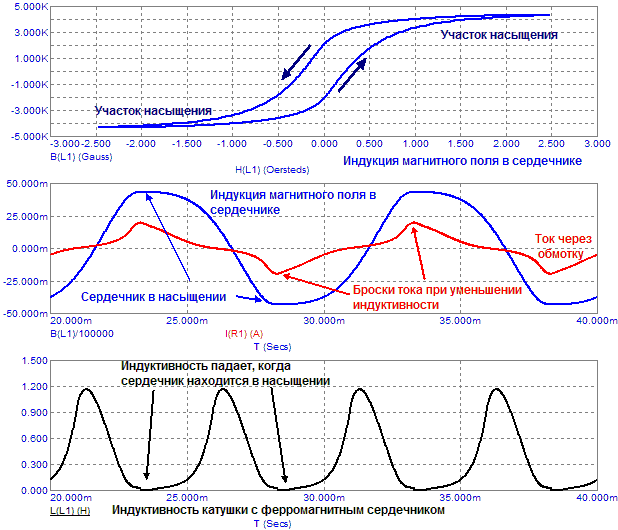
Рис.3. Процессы в индуктивности с ферромагнитным сердечником.
Казалось бы, что уменьшив амплитуду тока в цепи
катушки так, что сердечник перестанет насыщаться, мы устраним модуляцию величины
индуктивности и эта нелинейность исчезнет. Не тут то было 
.
Из-за наличия гистерезиса, при изменении напряженности МП, индукция в сердечнике
в определенные моменты остается на неизменном уровне, что также равносильно
уменьшению магнитной проницаемости сердечника, и, соответственно, резкому
падению мгновенного значения индуктивности. На следующих графиках этот процесс
можно рассмотреть подробнее.
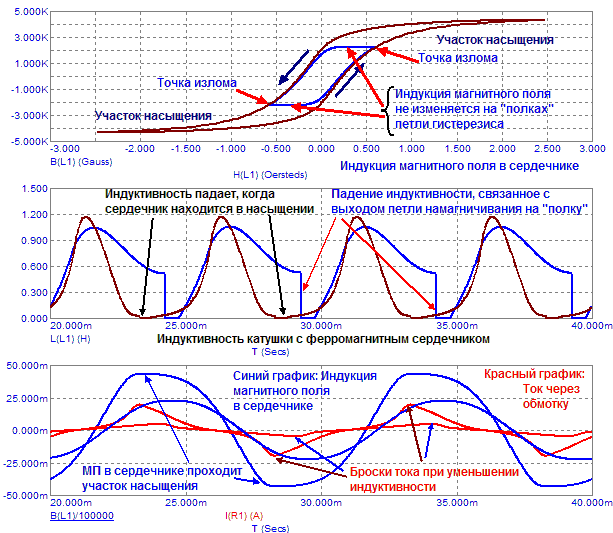
Рис.4.
В динамике сердечник находится под воздействием МП постоянного магнита, что приводит к тому, что МП от тока, протекающего по ЗК и проникающего в сердечник, изменяет индукцию в нем по частной петле гистерезиса. И, естественно, все нелинейные эффекты, описанные выше, сохраняются. Более подробно эти явления и способы борьбы с ними будут рассмотрены дальше на более конкретных примерах.
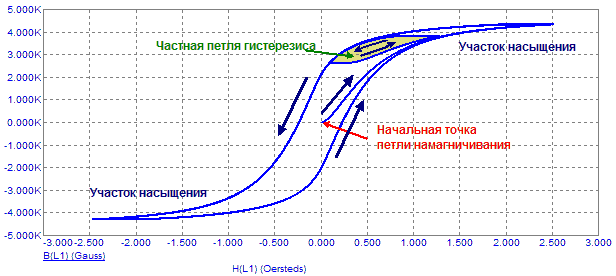
Рис.5. Частная петля гистерезиса.
3. Для определенности, в качестве материала магнитопровода возьмем электротехническую сталь с максимальной индукцией насыщения 2.2 Тесла, введем в магнитную систему воздушный зазор и дадим постоянное подмагничивание в 1 Тесла через дополнительную катушку. В качестве источника сигнала возьмем источник тока, который позволит оценить нелинейность импеданса, измерив искажения по напряжению на входных клеммах V(OUT). Вот результаты моделирования взаимодействия ЗК и такой магнитной цепи при частоте малого сигнала 2KHz:
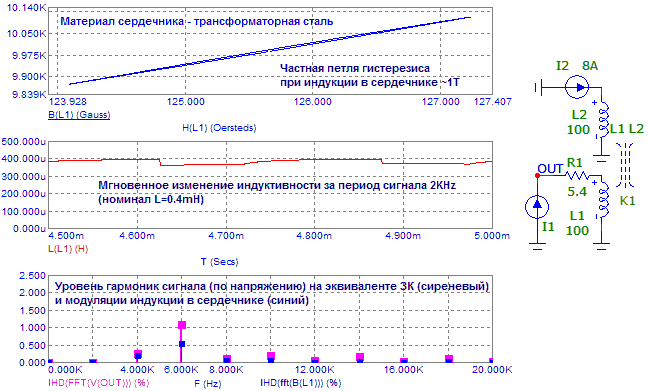
Рис.6.
А вот что показывают натурные замеры искажений (значение THD относится к желтому графику, остальные графики демонстрируют спектры искажений при снижении уровня сигнала на 10dB (THD=0.517%) и 20dB (THD=0.221%) соответственно):
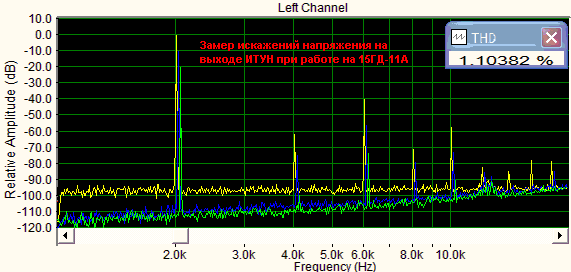
Рис.7.
Видно, что эти искажения не настолько малы, что ими можно
пренебречь. А по сравнению с искажениями современных УМЗЧ - они просто катастрофичны
. Один из способов
уменьшить этот вид искажений - применить токовое управление динамиком. Но
здесь мы не должны упустить из рассмотрения тот факт, что сила, возникающая
в "моторе" динамика, зависит не только от величины тока, но и от
мгновенного значения магнитной индукции в зазоре. Поэтому интересно с помощью
симулятора (а иначе - никак) взглянуть на искажения параметра B*I (смотрим
на формулу силы Ампера).
Для начала можно посмотреть, как влияет на искажения B*I уровень постоянного
подмагничивания в сердечнике (положение частной петли гистерезиса на кривой
намагничивания):
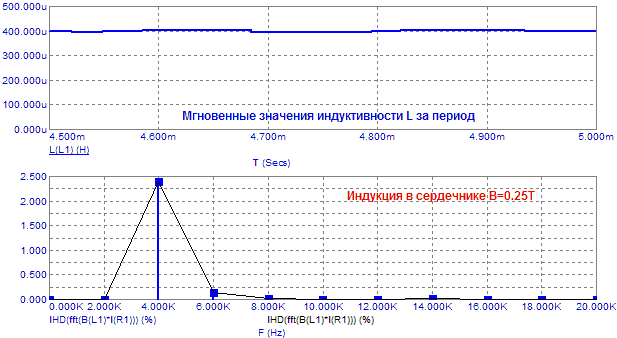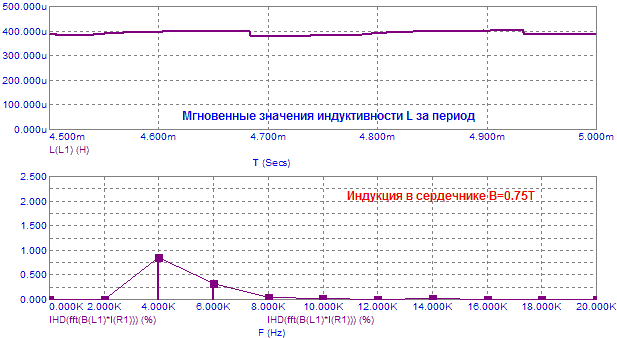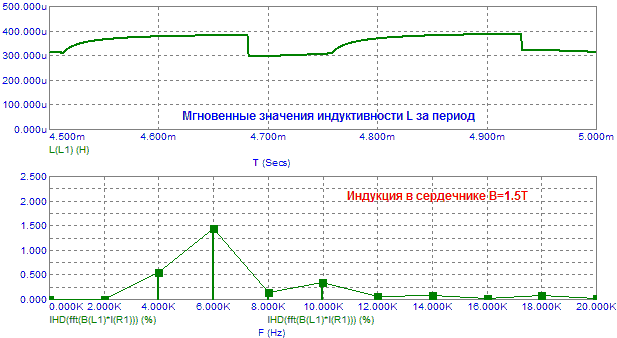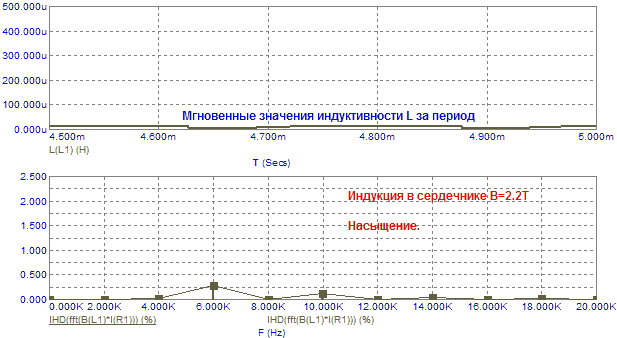
Рис.8. Зависимость искажений B*I от постоянного подмагничивания.
На последнем фрейме видно как падают индуктивность ЗК и уровень искажений при нахождении сердечника в полном насыщении. Естественно предположить, что от амплитуды сигнала также зависит уровень искажений B*I. Симулирование показывает, что уровень третьей гармоники мало изменяется, нарастает только вторая гармоника, хотя ток в цепи ЗК (черный график) имеет преимущественно доминирующую третью гармонику:
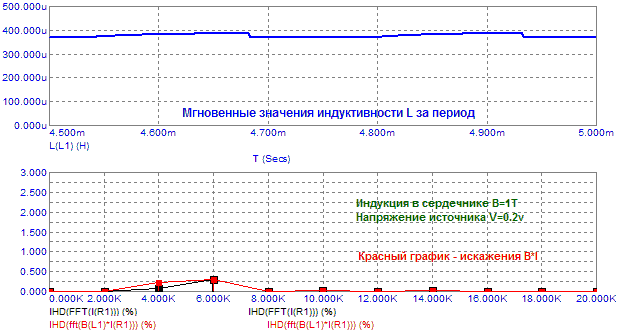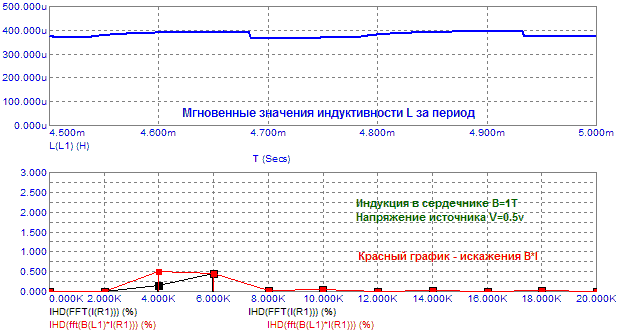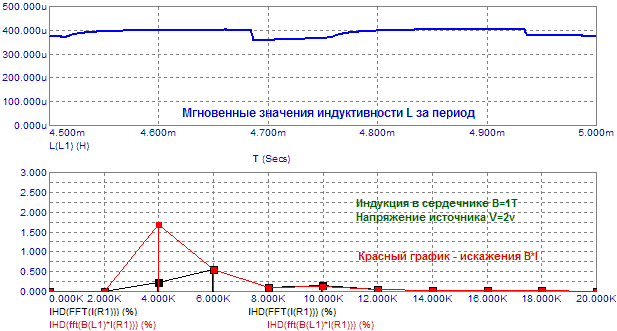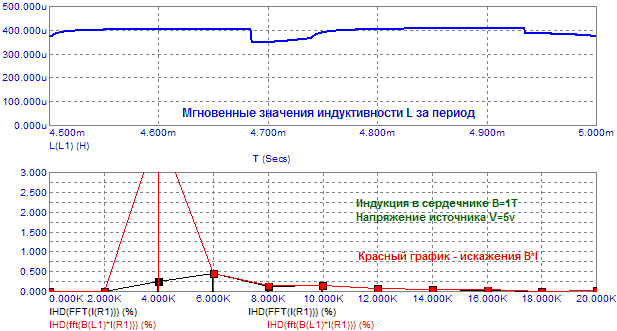
Рис.9. Зависимость искажений B*I от уровня синусоидального сигнала.
Сравним теперь величины возникающих искажений в случае традиционной запитки динамика от источника напряжения (ИНУН) и источника тока (ИТУН) при одинаковой силе тока в ЗК.
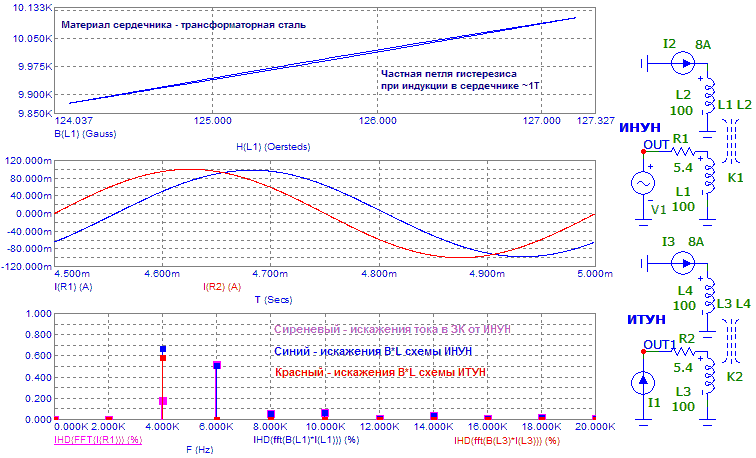
Рис.8. Сравнение искажений при питании ЗК от ИНУН и ИТУН.
Видно, что в случае ИТУН, вторая гармоника уменьшилась незначительно, а третья практически исчезла. Это во многом объясняет улучшения в звуке при использовании ИТУНа. Подобный характер поведения гармоник соблюдается в широком диапазоне уровней постоянного подмагничивания в сердечнике и амплитуд сигнального тока в отличие от случая с ИНУНом.
4. Для уменьшения влияния индуктивности ЗК в некоторых динамиках применяют короткозамкнутый виток, одеваемый на керн магнитопровода. Так как влияние индуктивности при работе с ИТУНом минимально, рассмотрим случай работы динамика от ИНУНа. Моделируется это просто добавлением обмотки с резистором. Но, что-то в модели положительное влияние КЗ-витка на искажения не так значительно...
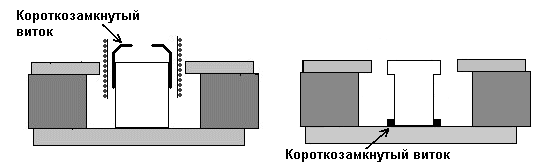
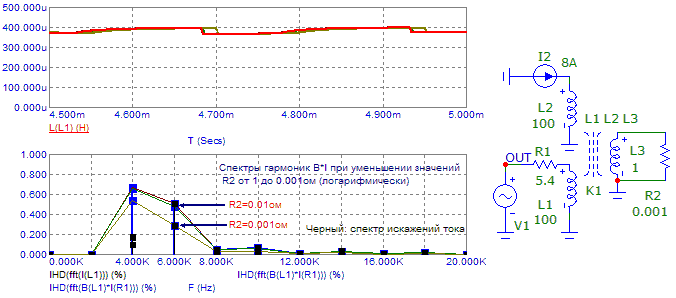
Рис.9. Влияние КЗ-витка на искажения.
Хотя общий импеданс ЗК при применении КЗ-витка, изготовленного из материала с высокой электропроводностью, например, меди, на высоких частотах достаточно хорошо выравнивается:
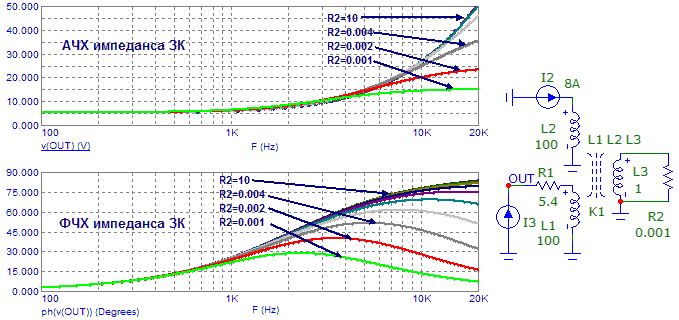
Рис.10. Влияние КЗ-витка на импеданс ЗК.
5. Известна технология AIC (ACTIVE IMPEDANCE CONTROL) или технология активной компенсации импеданса. Заключается она в использовании дополнительной неподвижной катушки индуктивности, расположенной на полюсе магнитной системы и включенной параллельно, но противофазно движущейся. За счет нее происходит "выталкивание" из магнитопровода переменной составляющей МП, генерируемой ЗК, что приводит к уменьшению нелинейных эффектов, связанных с наличием гистерезиса в магнитопроводе.
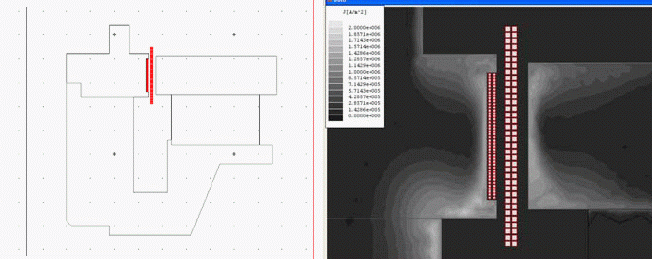
Рис.11. Конструкция магнитной системы и распределение МП.
В статье об AIC приведены результаты измерений,
подтверждающие снижение искажений при использовании этой технологии.
Ее применение со слов разработчиков дает следующие эффекты:
1. Линеаризация импеданса в рабочем диапазоне частот;
2. Линеаризация акустической и электрической фазы;
3. Значительное увеличение чувствительности и общего звукового
давления;
4. Уменьшение общего уровня гармонических искажений;
5. Стабильность передаваемой мощности.
Насчет 3 и 5 пунктов - не уверен, а вот 1, 2 и 4 пункты можно
проверить симулятором. К примеру - смотрим поведение ЗК в частотной области:
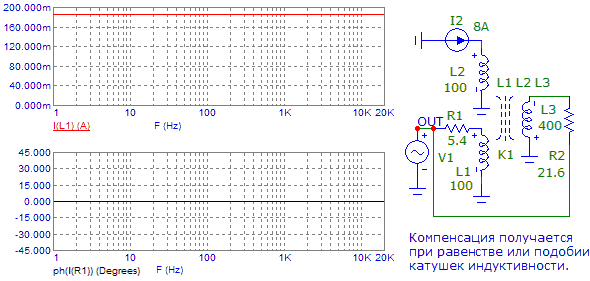
Рис.12. Суммарный импеданс ЗК.
В общем-то, в случае идеальной компенсации, имеем чисто активный импеданс звуковой катушки динамика. Кроме того, теоретически, можно добиться практически полного отсутствия искажений, возникающих за счет нелинейности магнитного сердечника:
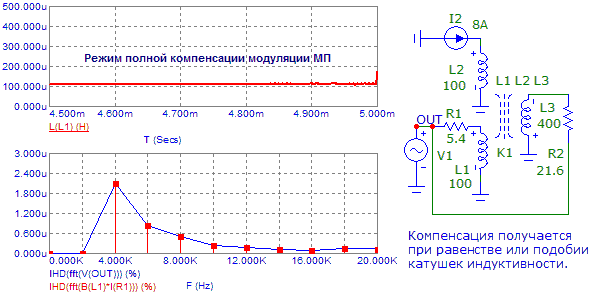
Рис.13. Искажения B*I при полной компенсации модуляции МП.
Конечно, при этом мы имеем определенные накладные расходы: приходится питать от выхода усилителя и дополнительную катушку. Но преимущества такого подхода должны перевешивать такой небольшой недостаток.
6. Заключение.
Хотя схемотехническое моделирование имеет определенные ограничения
и по точности моделей, и по тем упрощениям, которые мы ввели в начале статьи,
многое из процессов, происходящих в "моторе" динамика проясняется.
Основная причина проблем, как выясняется - это наличие петли гистерезиса магнитной
цепи, характеризующая степень сопротивляемости ферромагнетика к перемагничиванию,
физически связанная с затратой энергии на переориентацию магнитных доменов
в веществе. При этом мгновенная эффективная магнитная проницаемость материала
падает, что приводит к возникновению искажений в динамике, как через амплитудную
нелинейность импеданса, так и через нелинейность модуляции магнитного поля
в сердечнике.
Напрашивается аналогия со специфическим видом искажений - "Memory
Distortion" (искажения, связанные с предысторией сигнала/системы),
которые практически невозможно скомпенсировать. Неплохим методом уменьшения
этих искажений в месте их возникновения, является использование токового управления
ЗК динамика. Свести к нулю этот вид искажений можно только полностью устранив
сигнальную модуляцию МП в ферромагнетике. Короткозамкнутый виток частично
решает эту задачу. Технология AIC теоретически позволяет это сделать наиболее
полно. Хотя, никто не мешает придумать свои методы решения этой проблемы
