Групповое время задержки

Меня удивило практическое отсутствие цельной информации по этому вопросу в интернете... Особенно, применительно к области звукотехники. Каждый, в меру своей сообразительности и опыта, пытается трактовать ГВЗ по-своему Как-то захотелось привести этот вопрос к общему знаменателю, с позиции здравого смысла
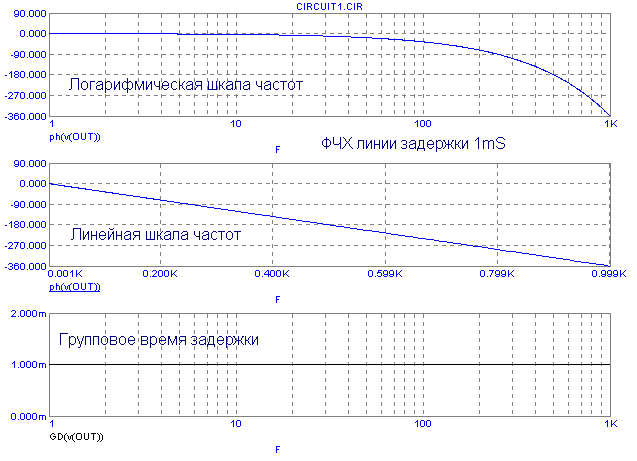
А для этого давайте попробуем прояснить физическую суть этого, казалось бы, абстрактного термина. Формально, по определению - это производная фазы по частоте, геометрически - тангенс угла наклона к касательной в выбранной точке на графике ФЧХ. Рассмотрим этот момент подробнее на примере ФЧХ линии задержки в 1mS. Ниже на графиках показаны графики фазы такого звена на логарифмической и линейной шкалах частот. Естественно, для линии задержки фаза сигнала будет линейно отставать с ростом частоты. Видно, что на частоте 1KHz набег фазы составил 360градусов или 2*Pi радиан. Для круговой частоты 2*Pi*1000 рад/сек, ГВЗ составит (2*Pi)/(2*Pi*1000)=0,001S=1mS. Что и не удивительно . Для любой другой частоты мы получим ту же самую величину, так как график ФЧХ линеен на линейной шкале частот, что и подтверждает симулятор на третьем графике (GD). Поэтому сигнал любой формы пройдет через такое звено (линию задержки) без искажений, просто будет задержан по времени.

В случае же электроакустического тракта, имеющего различное ГВЗ на различных частотах (а это чаще всего имеет место в жизни), произойдет искажение формы нестационарного или негармонического сигнала из-за явления, называемого дисперсией - все гармоники такого сигнала будут задержаны на различное время, в отличие от стационарного гармонического сигнала, для которого понятие ГВЗ, вообще-то говоря, неприменимо. Для него мы просто будем иметь на выходе ту же синусоиду, но сдвинутую по фазе относительно входного сигнала . Рассмотрим типичный пример негармонического процесса - прохождение прямоугольного импульса через ФНЧ.

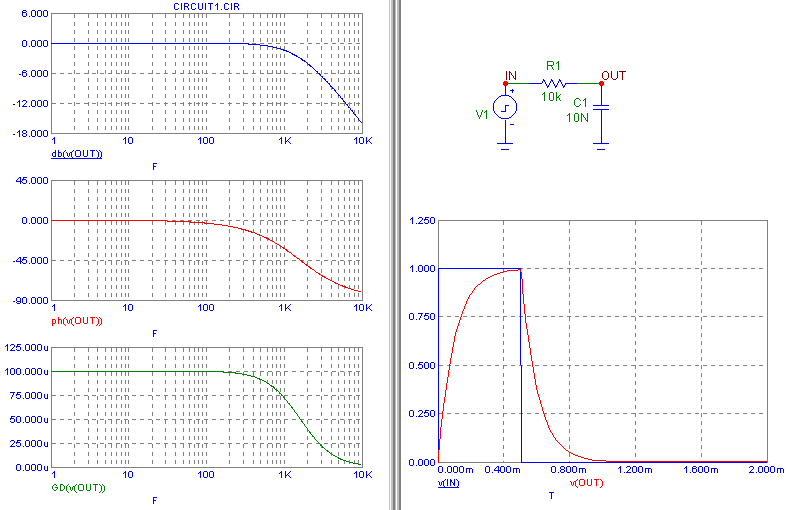
Видим, что исказилась не только форма сигнала, но и как бы произошла задержка "тела" импульса по времени. Неожиданное, на первый взгляд, поведение графика ГВЗ такой цепи объясняется просто, если взглянуть на форму графика ФЧХ того же RC-звена, но при линейной шкале по частоте. Ведь, по определению ГВЗ как производной фазы по частоте - геометрически - это тангенс угла наклона касательной к точке фазового графика на выбранной частоте.

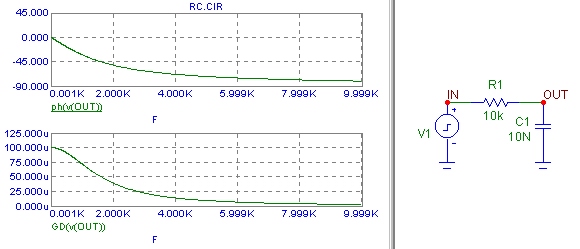
  В своих поисках в интернете, наиболее близкое к моему пониманию этого явления, нестрогое определение ГВЗ я нашел тут:
"Групповое время задержки - энергетическое понятие, пришедшее из квантовой электродинамики, где оно играет определяющую роль. Оно соответствует скорости распространения центра тяжести энергии волнового пакета. Для звука важна не энергия волнового пакета, а деформация сигналограммы начального переходного процесса - атаки, а это, как говорят в Одессе, "две большие или четыре маленькие разницы". Вообще задача звуковоспроизведения, как любого воспроизведения, чего бы то ни было изначально данного, состоит в копировании этого данного."
  Ценные слова . Вот, давайте и рассмотрим как проходит "деформация сигналограммы начального переходного процесса - атаки" в электроакустическом тракте.
  В акустических системах (АС) наибольшим ГВЗ, как правило, обладает НЧ-звено. Не зря же говорят о "задержке баса" . Логично предположить, что оно вносит максимальные "деформации" такого рода. Для примера, рассмотрим прохождение волнового пакета через АС типа "закрытый ящик" (ЗЯ) с частотами среза 50Hz и 25Hz. Как известно, его АЧХ соответствует АЧХ ФВЧ 2-го порядка. Ниже приведены графики АЧХ, ФЧХ и ГВЗ (GD) для них обоих.

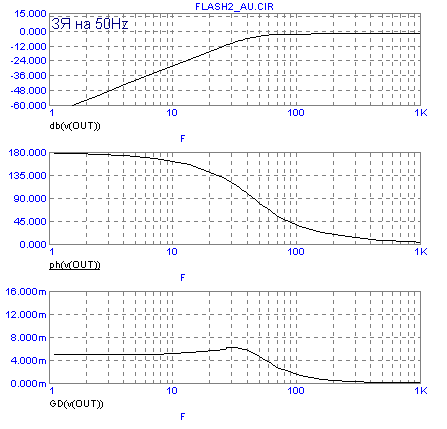
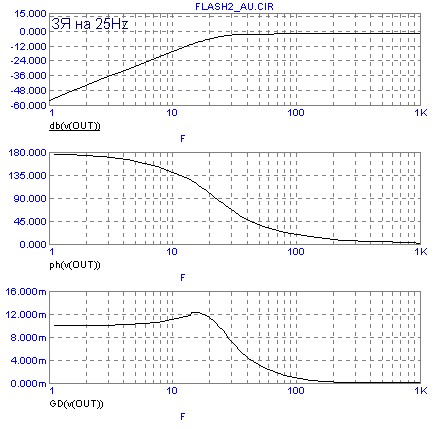
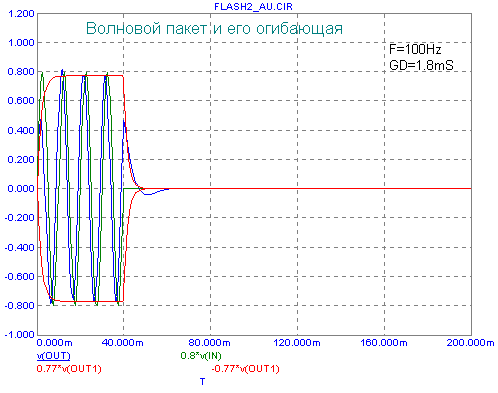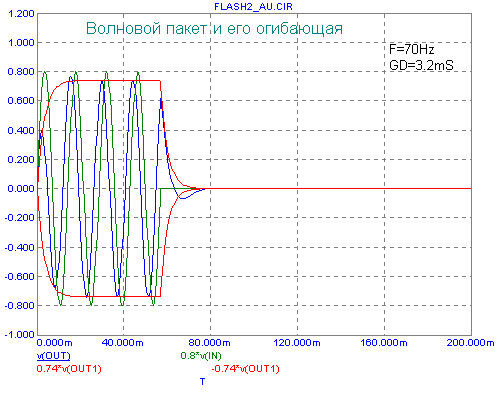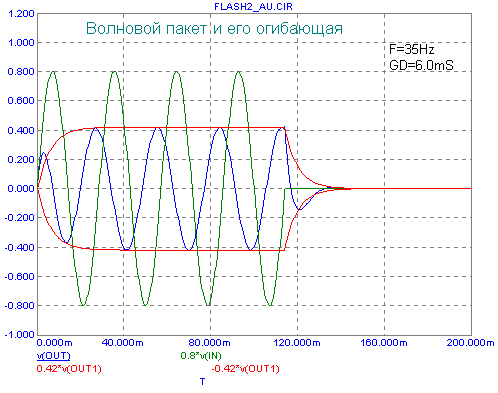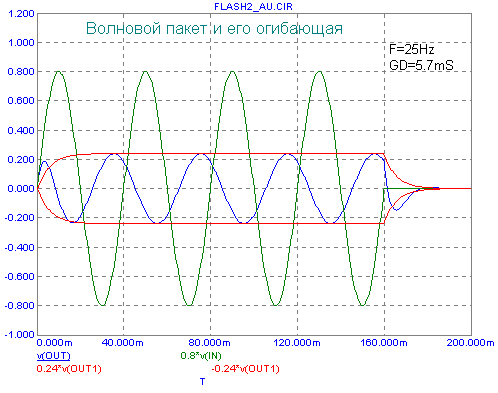
При моделировании во временной области рассмотрим прохождение волнового пакета из 4-х периодов синусоиды (ToneBurst) нескольких фиксированных частот - 100, 70, 50, 35, 25Hz (графики зеленого цвета). Огибающая сигнала моделировалась прохождением прямоугольного импульса, соответствующего закону модуляции, через RC-звено, с постоянной времени, равной ГВЗ для соответствующей частоты заполнения (графики красного цвета). Выходной сигнал (SPL) - графики синего цвета. Примечание - для большей наглядности, необходимо, чтобы в свойствах вашего броузера была включена опция показа анимированной графики. Первая осциллограмма приведена для модели АС ЗЯ с частотой среза 50Гц -

А это - для АС ЗЯ с частотой среза 25Гц -

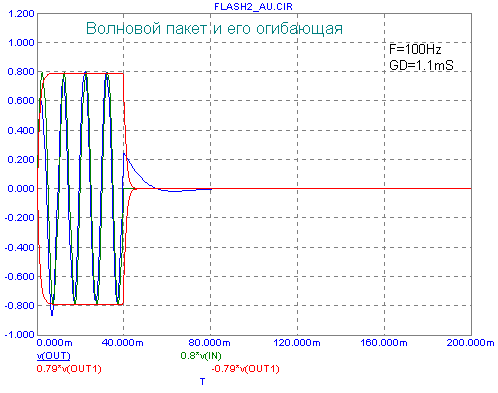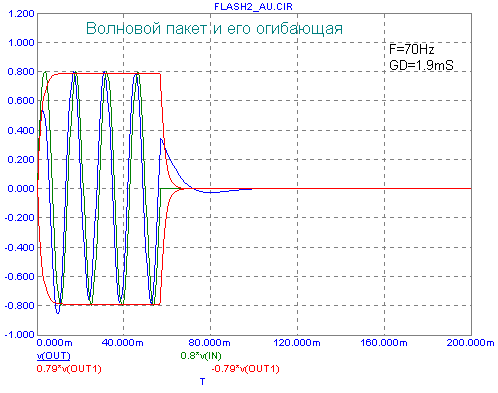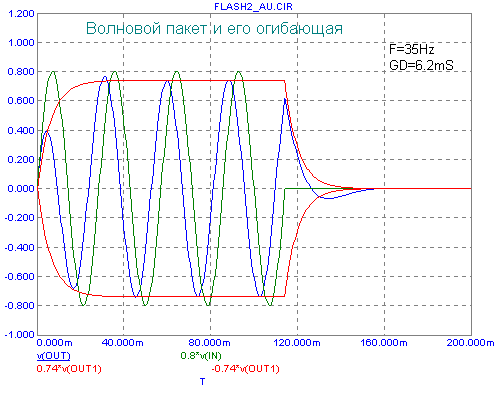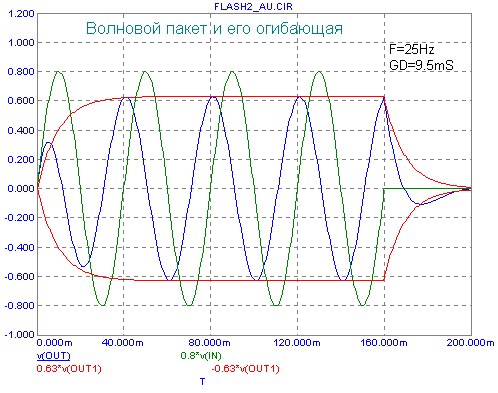
Рассмотрение графиков для многих прояснит кажущееся противоречие между положительным фазовым сдвигом сигнала (на опережение) и нарастающей ГВЗ (отставание) по мере уменьшения частоты. Все просто - фазовый сдвиг относится к частоте заполнения сигнала ToneBurst, а ГВЗ - описывает задержку огибающей сигнала. Таким образом, строя акустическую систему с меньшим ГВЗ, мы автоматически улучшаем характер переходных процессов в АС на НЧ. Наглядно видно, что АС с более низкой частотой среза вносит гораздо меньшую "деформацию" в атаку сигнала, да и в его уровень...
Можно было бы еще рассмотреть АС фазоинверторного типа, для которых ГВЗ более актуально, но, к сожалению, у меня нет ее электроакустической модели ... А ведь это могло бы внести некоторую ясность в постоянные споры между сторонниками того или иного типа акустического оформления .

Кстати, по порогам заметности фазовых искажений (и ГВЗ) на просторах интернета мне встретилась статья "ВОСПРИЯТИЕ ФАЗОВЫХ ИСКАЖЕНИЙ В ОБЛАСТИ ЧАСТОТЫ ОСНОВНОГО РЕЗОНАНСА ГОЛОВКИ ГРОМКОГОВОРИТЕЛЯ", к которой приложил руку сам АМЛ . Так что, интересующиеся могут продолжить знакомство с вопросом.

Групповое Время Задержки

(ГВЗ или Group Delay)